DSA (CP 213) UE 2022-2023

Data Structures and Algorithms Analysis Exam - CP 213

University of Dodoma
College of Informatics and Virtual Education
Department of Computer Science and Engineering
End of Semester One University Examination for the 2024/2025 Academic Year

Course Name: Data Structures and Algorithms Analysis
Paper Code Number: CP 213
Date of Examination:
Time: 08:00-11:00
Duration: 3 Hours
Venue(s): AUDITORIUM & LRB 102

Sitting Programme(s): BSc. CS2, SE2, CNISE2, CE2, TE2, CSDFE2, IS2, MATH2 & CARRYOVER.

---

SECTION A (40 Marks)

Question One

Choose the correct answer for each of the following items. Fill the answer in a table format like the one presented here under.
[1 Mark each]

i	ii	iii	iv	v	vi	vii	viii	ix	x

i. Suppose you have the following function prototype and variable declaration:
void func(int a[]);
int x[10];

Which is the correct way to call the function with x as the argument?
a. func(x);
b. func(x[]);
c. func(x[10]);
d. func(&x);

ii. Consider the following statements:
int *p; int i; int k; i = 42; k = i; p = &i;

Which of the following statements will change the value of i to 75?
a. k = 75;
b. *k = 75;
c. p = 75;
d. *p = 75;

iii. Given the following function header, which statement is wrong?
void read(const int *value);
a. int j = *value;
b. cout << (*value + 2); c. cin>>*value; d. All of the above

iv. What is the maximum depth of recursive calls a function may make?
a. 1
b. 2
c. n (where n is the argument)
d. There is no fixed maximum

v. Considering the following function:

void test_a(int n) {
    cout << n << " ";
    if (n > 0) {
        test_a(n - 2);
    }
}

What is the output when the call test_a(4) is made?
a. 0 2 4
b. 0 2
c. 2 4
d. 4 2

vi. Suppose T is a binary tree with 14 nodes. What is the minimum possible depth of T?
a. 0
b. 3
c. 4
d. 5

vii. Select the one FALSE statement about binary trees:
a. Every binary tree has at least one node.
b. Every non-empty tree has exactly one root node.
c. Every node has at most two children.
d. Every non-root node has exactly one parent.

viii. What additional requirement is placed on an array so that binary search may be used to locate an entry?
a. The array elements must form a heap.
b. The array must have at least 2 entries.
c. The array must be sorted.
d. The array’s size must be a power of two.

ix. In a selection sort of n elements, how many times is the swap procedure executed in the complete execution of the algorithm?
a. 1
b. n - 1
c. n log n
d. n²

x. What is the worst-case time for quick sort to sort an array of n elements?
a. O(log n)
b. O(n)
c. O(n log n)
d. O(n²)

---

Question Two

a. Given the variable declaration float price;, write down another statement that will create a pointer pointing to the variable price.
[2 Marks]

b. Write a statement that declares a constant pointer ptrCount initialized with new int[103].
[2 Marks]

c. What does the following pair of statements mean?

const char gender = 'F';
const char *ptr = &gender;

[2 Marks]

d. What will be the output of the following code section?

void func(int *num) {
    *num += *num;
}
 
int number = 11;
cout << "Initial Value: " << number;
func(&number);
cout << "Final Value: " << number;

[2 Marks]

---

Question Three

a. Given the following structure, write a single statement that declares a variable part1 of type Part and initialize its fields.
[3 Marks]

struct Part {
    int partNumber;
    float cost;
};

b. Write down a loop that will create Part pointers (using new) and store them at the indices of a 10-sized array called parts.
[2 Marks]

c. What happens when the new operator is called while there is no memory on the heap?
[2 Marks]

---

Question Four

a. Illustrate diagrammatically how a queue-based array of size 5 will look after each of the following sequence of queue operations:
enqueue(5); enqueue(4); dequeue(); dequeue(); dequeue(); enqueue(3); enqueue(2); dequeue(); enqueue(1);
[6 Marks]

b. Given an integer array of size 13, write down a function called sum that will sum all items in the array and return the total.
[3 Marks]

c. Assuming an array-based stack S of size n, write down the code for pop and push procedures.
[6 Marks]

---

SECTION B (60 Marks)

Question Five

a. Briefly explain the three features that are considered when designing sorting algorithms.
[6 Marks]

b. Given the following array, how will it appear after the first six (6) iterations of the insertion sort algorithm?
{14, 6, 9, 1, 4, 15, 12, 5, 6, 7, 11}
[6 Marks]

c. Write down the code for a function implementing the recursion-based binary search algorithm that operates on an array collection.
[8 Marks]

---

Question Six

a. Given the infix expression ((a + b) * (c - d)) / (e + f), employ the respective algorithm to produce the postfix expression. Clearly show your work.
[8 Marks]

b. Evaluate the following prefix expression: /-ab*c-def given that a = 24, b = 10, c = 7, d = 6, e = 4, f = 3.
[8 Marks]

c. Write a piece of code that checks whether a linked list-based queue is empty or not.
[4 Marks]

---

Question Seven

Study the tree shown in Figure 1 and answer the questions that follow.

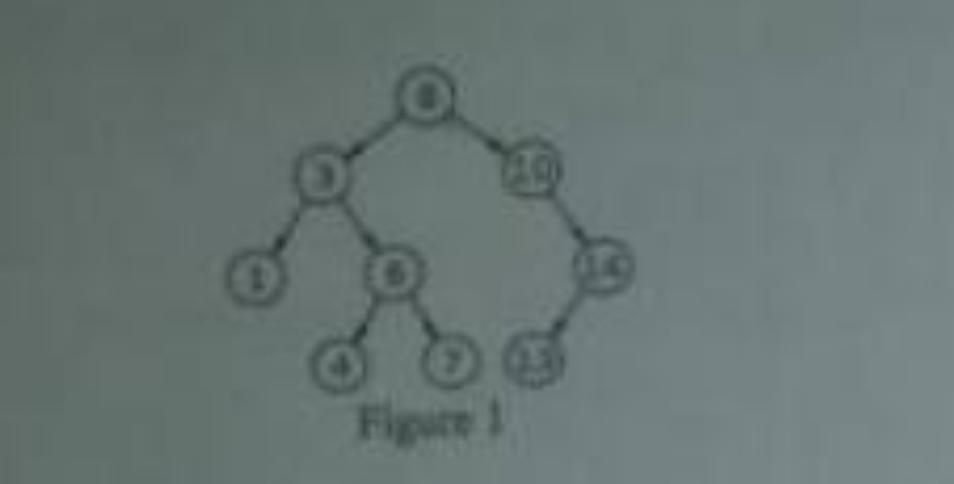Figure 1

a. What is the type of the tree shown? Justify.
[2 Marks]

b. Find the height of the tree.
[1 Mark]

c. Write down the pre-order, in-order, and post-order traversal of the tree above.
[9 Marks]

d. Develop an algorithm (pseudo code) that will employ pre-order traversal to search for a node in the tree.
[8 Marks]

---

Question Eight

a. Using the graph shown in Figure 2, list down the order of vertices when the graph is traversed depth-first and when it is traversed breadth-first. In each case, assume 0 is the starting point. Depict each traversal on a tree.
[10 Marks]

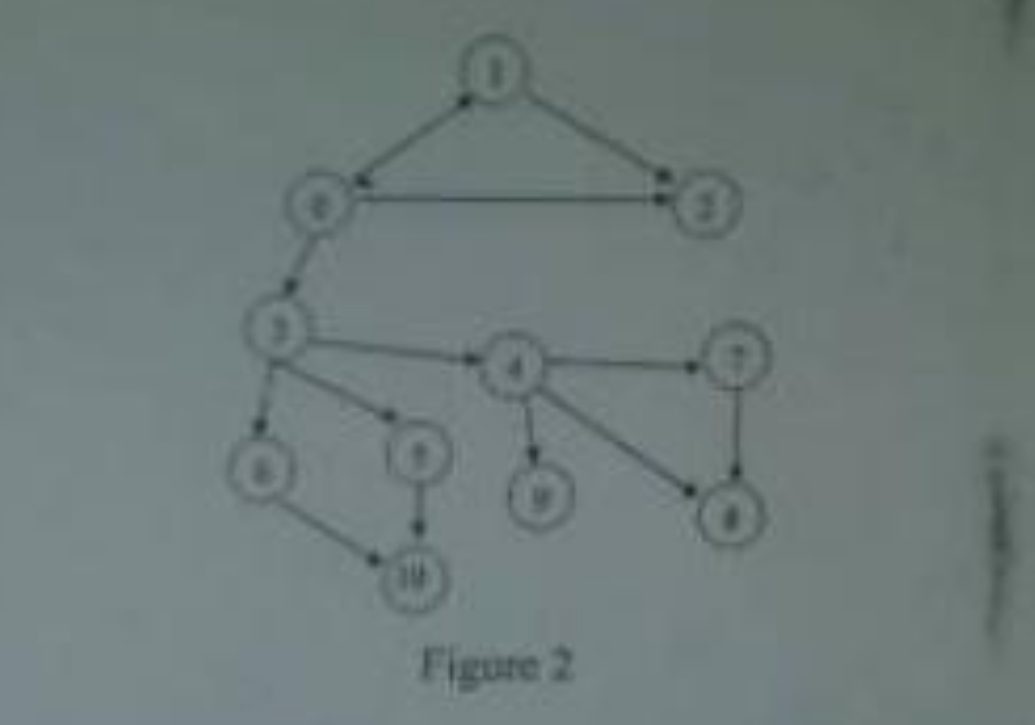
Figure 2

b. Write a program that uses a structure of your choice equipped with a node pointer to create a dynamic memory linked list. Design your code so that the procedure of adding a node into the list falls into a separate function.
[10 Marks]